Uma viga em balanço, afilada, de seção reta quadrada, suporta uma carga concentrada na extremidade livre. A largura e altura da viga variam linearmente de na extremidade livre a na extremidade engastada. O comprimento da viga é . Determine a tensão normal máxima devido á flexão
Passo 1
Para resolver a questão precisamos aplicar a equação da flexão. Porém, o momento e a geometria mudam com a distância. Então faremos o seguinte procedimento:
- Encontramos uma equação para o momento fletor
- Encontramos uma equação para o momento de inércia
- Aplicamos a equação da flexão
- Encontramos o valor da tensão em um ponto conhecido, neste caso, o engaste
- Determinamos a função para o raio
Passo 2
Vamos fazer uma seção na figura e calcular o momento fletor nesta seção:
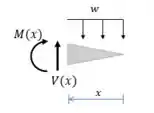
Passo 3
Agora vamos determinar expressões que representem as propriedades geométricas:
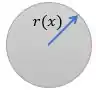
Passo 4
Vamos aplicar na fórmula da flexão
Passo 5
Sabemos que a tensão é constante em qualquer ponto da viga. Mas qual o valor desta tensão? Bem, o único ponto em que podemos calcular isso é o engaste, já que é o único ponto em que conhecemos todas as propriedades.
No engaste: e
Sabemos então que este é o valor da tensão para qualquer valor de
Passo 6
Vamos igualar agora o valor da tensão com a equação da tensão:
Isolando o