Uma viga simples de seção retangular (largura , altura ) suporta uma carga uniforme de num vão de . Achar as tensões principais numa seção a do apoio esquerdo: (a) no eixo neutro; (b) acima do eixo neutro e (c) no topo da viga.
Passo 1
Primeiro, vamos calcular os esforçoes cortantes e os momentos fletores da viga.
Como atua somente uma carga distribuída na viga, o esfroço cortante nela terá mesmo módulo.
Onde o ponto de referência para o cálculo é o próprio ponto (ou ).
Passo 2
Agora, vamos calcular o centroide da seção transversal. Sabemos que o centroide é dado pela média ponderada das áreas retangulares e seus respectivos centroides no eixo.
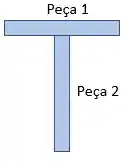
Passo 3
Devemos, então, calcular o momento de inércia da seção transversal. Sabemos que para seções retangulares, temos a seguinte equação de momento de inércia:
Onde é o tamanho da parede paralela ao eixo e é o tamanho da parede perpendicular ao eixo.
Neste caso, devemos usar o Teorema dos Eixos Paralelos, pois os centroides das peças separadas não estão no mesmo eixo que o centroide da peça total, o qual é dado por:
Onde é a área de um elemento separado e é a distância do seu centroide com o centroide da peça total.
Portanto, de acordo com o desenho do passo anterior:
Onde, temos que:
E assim, ficamos com:
Passo 4
Como nossos cálculos anteriores são comuns aos dois pontos pedidos no enunciado, iremos dividir a questão, resolvendo primeiro o que foi pedido para o ponto e depois para o ponto .
Cálculo da tensão no ponto :
Cálculo da tensão máxima de cisalhamento no ponto :
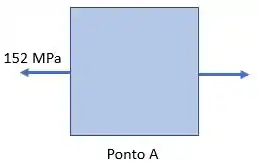
Passo 5
Calcularemos, então, as tensões principais no ponto :
E ficamos com duas tensões, e :
Passo 6
Fazendo as contas agora, para o ponto , temos:
Cálculo da tensão no ponto :
Cálculo da tensão máxima de cisalhamento no ponto :
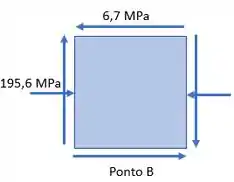
Passo 7
Cálculo das tensões principais no ponto :
Novamente obtemos duas tensões, e :
Passo 8
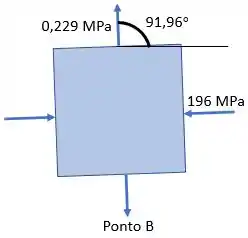
Calcularemos, agora, o ângulo que o elemento será rotacionado, com os valores que obtivemos no
E devemos calcular o arco tangente do valor encontrado:
Esse ângulo é quanto um dos eixos está deslocado. Para encontrar o outro ângulo, devemos somar noventa graus com :
Passo 9
Por fim, devemos descobrir qual ângulo corresponde ao eixo de tensão normal. Podemos descobrir isso pela fórmula:
Logo, achamos que corresponde ao eixo de tensão normal, responsável por
Resposta
As tensões principais no ponto são:
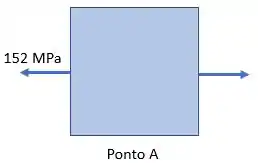
E as tensões no ponto são: