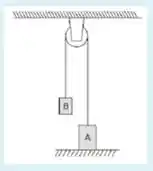
São conectados dois corpos por um fio leve que passa sobre uma polia leve sem atrito. O corpo B de está a do solo e é solto do repouso. Utilizando a lei de conservação de energia, determine a velocidade escalar (em ) do corpo de , que inicialmente está no solo e tem massa , no momento que o corpo B atinge o solo. Se precisar, utilize .
Passo 1
Fala galera, tudo beleza?
No começo do movimento temos apenas a energia potencial gravitacional do corpo , pois ele está suspenso. O corpo está no chão (então sem energia potencial gravitacional) e em repouso (sem energia cinética), então nesse instante esse corpo não contribui com energia pro sistema.
Quando o corpo chega no chão, ele troca toda sua energia potencial em energia cinética. Mas ele não troca só pra ele, ele dá também energia cinética pro corpo que sai do chão e se move pra cima. O corpo também tem energia potencial gravitacional no momento em que atinge o chão.
Então as energias que a gente tem aqui são:
Lembrando que a velocidade escalar de é igual a velocidade escalar de , pois o sistema de move junto. Não há deslizamento na polia.
Passo 2
Vamos começar calculando a energia inicial do sistema, ou seja, a energia potencial gravitacional do corpo B.
A energia potencial de é:
A massa é e a altura , considerando a energia inicial do sistema é:
Passo 3
Agora vamos calcular a energia potencial gravitacional do corpo A. ele sobe a mesma altura em que o B estava, então aqui segue sendo . A massa do corpo A é . Então a energia potencial de A é:
Passo 4
As energias cinéticas de A e de B respectivamente são:
e
Passo 5
E agora partiu jogar todos esses resultados na equação de conservação?
Lá do passo um:
Agora coletando os resultados:
Agora ficamos com uma equação apenas para a velocidade! Vamos resolver juntos?
Ufa! Terminamos! A velocidade com que o corpo A tem quando B chega ao chão é .
Espero ter te ajudado!
Bora pra próxima?