Considere as funções deriváveis e cujos gráficos estão esboçados abaixo:
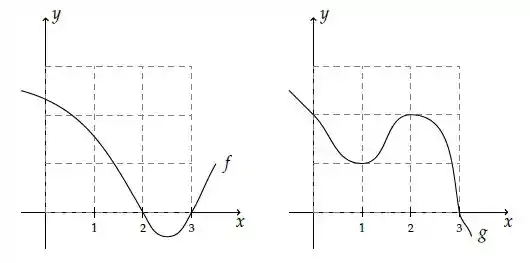
Seja . Sabendo que é ponto de mínimo local de e que , é correto afirmar que
- é ponto de inflexão de
- é ponto de mínimo local de
- é ponto de máximo local de
Passo 1
Oi pessoal, tudo bem por aí? Essa questão nos dá esses dois gráficos aqui
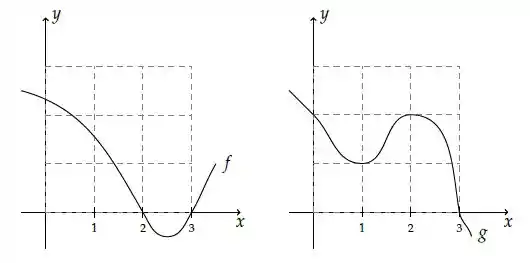
Notem que são de duas funções diferentes: e . E elas estão ligadas por isso aqui
elas fazem parte de uma outra função! Aí o problema faz uma série de afirmações sobre a derivada de e se esse ponto é de máximo, mínimo etc...
E agora, como resolver isso?

Quando temos uma função composta, para achar sua derivada precisamos usar a regra da cadeia
Como então a derivada de em é
Então temos que
Sabemos também que um ponto de máximo é quando a derivada passa de valores positivos para negativos. E que o de mínimo é o contrário!
Sendo assim, a ideia é tirar as informações das derivadas dos gráficos dados e determinar o que esse ponto significa na função !

Relaxa, vou fazer contigo!
Bora lá!
Passo 2
A derivada de é
Daí sabemos que tem um mínimo local em , então
Assim a derivada de é zero
Então podemos descartar como resposta as letras (a) e (b)
Beleza?

Passo 3
Agora vamos observar as duas funções em torno do ponto , para ver quais os sinais das derivadas de cada uma e assim, determinar o sinal da derivada de em torno desse ponto. Com isso vamos poder dizer se é máximo, mínimo ou inflexão.
Nossa derivada
Antes desse ponto (retas em azul ) temos
as duas derivadas são negativas, assim a derivada de fica positiva
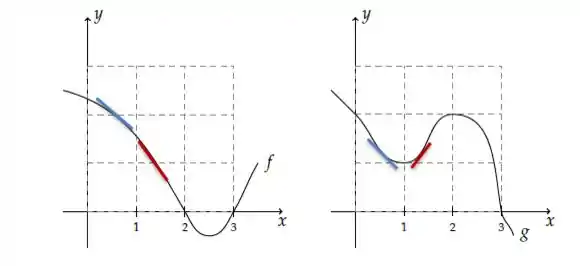
E depois desse ponto a segue tendo derivada negativa e a positiva, assim o produto delas fica negativo
Então temos que o valor da derivada de em torno de passa e valores positivos para negativos, sendo, portanto, um ponto de máximo local
Alternativa correta (e)
E é isso! Até a próxima!