Enunciado
Mecânica dos Sólidos - Timoshenko - Mecânica dos sólidos - Vol 1- Ed: 1º - Capítulo 1.8 - Ex. 9
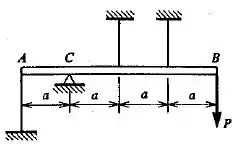
A barra rígida , representada na figura, está simplesmente apoiada em e carrega uma carga na extremidade . Três fios idênticos, de material elástico-plástico suportam a barra. Calcular a carga de escoamento, , e a carga limite, , sabendo que a área da seção transversal dos fios é .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Apesar desta ser a última questão do tópico 1.8, ela não é tão difícil quanto parece.
Temos que determinar aqui a carga de escoamento e a carga limite .
Para vocês verem que a questão não é tão difícil assim, vamos começar determinando quem é a carga de escoamento!
Esta carga é tal que o fio começa a escoar. Portanto, se ele tem um limite de escoamento , por definição temos:
Passo 2
Bom, agora que determinamos a carga de escoamento, vamos para a carga limite. Esta é a carga que ocorre quando todos os fios escoarem.
Então, ao fazermos o diagrama de corpo livre, teremos:
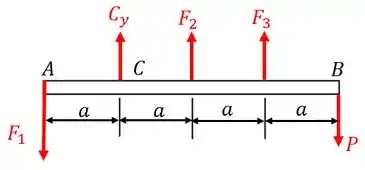
Pela estática, fazendo o somatório dos momentos em torno de , obtemos:
Como a carga limite é atingida quando todos os fios escoam, então temos . Portanto,
E assim finalizamos a questão!