Enunciado
Mecânica dos Sólidos - Timoshenko - Mecânica dos sólidos - Vol 1- Ed: 1º - Capítulo 1.8 - Ex. 7
Achar a carga limite, , da estrutura representada na Fig. 1-19a, sabendo que o material é elástico-plástico e que a área da seção transversal do fio vertical é o dobro da dos fios inclinados. Fazer ; e a área do fio vertical .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Temos que determinar qual a carga em que toda a estrutura entra no regime plástico, a chamada !
E para a nossa alegria, as relações das forças já foram obtidas no Exemplo 1 da seção 1.6 e até discutida uma questão quase idêntica a essa nossa na seção 1.8! Que coisa excelente, não?
Para início de questão, precisamos determinar qual a barra que irá escoar. Na teoria deverá ser a barra , pois ela está submetida a uma maior força! Entretanto, como a área das outras duas barras são menores, talvez tenhamos algo diferente aqui.
Sendo assim, vamos começar calculando as tensões das barras como função de (usando as relações descritas nessas seções anteriores). Desta forma, temos:
Portanto, como , então, a primeira barra a escoar realmente é a barra vertical!
Passo 2
Como já sabemos que a primeira barra a escoar é a barra vertical, ela atingirá uma força .
À medida que aumentamos a força , a força permanece constante enquanto a força aumenta. Para calcularmos a força , basta analisarmos o diagrama de equilíbrio em relação ao nó , como pode ser observado na figura abaixo:
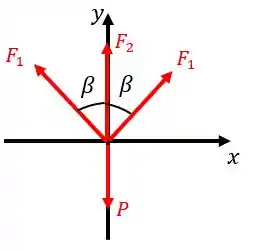
Então, como temos equilíbrio , chegamos a seguinte relação para a força :
Como a carga limite é obtida quando toda a estrutura escoa, temos que fazer as barras inclinadas escoarem. Para isto, é necessário que (a área das barras inclinadas é ).
Então, substituindo esta relação, iremos obter:
E assim finalizamos a questão.