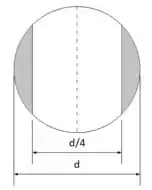
Uma barra de seção transversal circular tem um furo radial, conforme mostra a figura, com diâmetro igual a . Supondo que a tensão admissível seja , calcular a carga provável, , que a barra pode suportar sob tração.

E aí galera, vamos resolver mais uma?

Inicialmente calcularemos a área hachurada. A área é composta por dois segmentos circulares simétricos. Então, é só calcular um e multiplicar por 2, blz?

A área de um segmento circular é dada por:

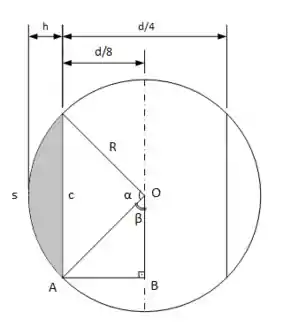
Como não temos o ângulo , vamos encontrar ele utilizando o triângulo OAB em função do ângulo :

Agora calcularemos a área de uma seção hachurada:

Cuidado! O primeiro é em radianos ....

Multiplicamos a área encontrada por 2