Enunciado
Mecânica dos Sólidos - Timoshenko - Mecânica dos sólidos - Vol 1- Ed: 1º - Capítulo 1.10 - Ex. 2
Calcular a energia de deformação na barra vista na Fig. 1-7, sendo a área da seção transversal e o módulo de elasticidade.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Vamos começar relembrando a Figura 1-7 abaixo.
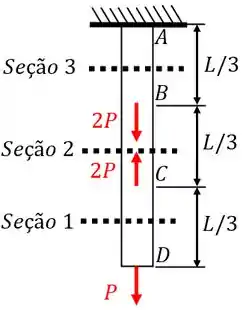
Como pode ser visto, ela está submetida a forças e em pontos específicos da nossa barra.
Como queremos calcular a energia de deformação total dela, teremos que utilizar a seguinte relação:
Mas é só isso? Basta aplicarmos esta relação? Bom, a resposta é sim e não ao mesmo tempo. Basta usarmos a relação sim, mas, para isto, temos que entender um pouco a força sobre cada seção da barra (indicadas na nossa figura anterior!).
Portanto, temos que determinar a força submetida sobre cada uma das seções e calcular a energia de deformação resultante devida a esta força! Importante lembrarmos que os comprimentos consistem no comprimento total da seção!
Sendo assim, vamos aos cálculos!
Passo 2
Vamos começar pela seção 1, indicada na figura do Passo 1. Desenhando o diagrama de equilíbrio, temos:
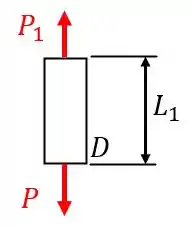
Portanto, como a barra está em equilíbrio , então, a força é igual a e a energia de deformação devido a esta seção será:
Agora, basta repetirmos para as outras seções! Esboçando o diagrama de equilíbrio para a seção 2, temos:
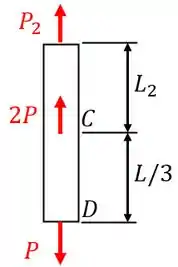
Para a seção 2, aplicando a relação de equilíbrio, obtemos . Portanto, a deformação devido a esta seção será:
Por fim, para a seção 3 temos o seguinte diagrama:
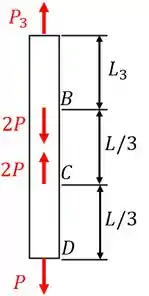
Sendo a força . Portanto, a energia de deformação será:
Passo 3
Para finalizarmos a questão, basta somarmos as energias de deformações de cada seção. Portanto,
E assim finalizamos a questão!