Calcular a tensão máxima de cisalhamento na viga do Problema 5.1.9
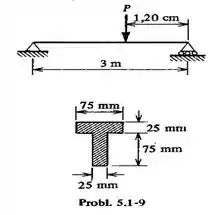
Passo 1
Fala aí! Queremos a tensão máxima. Então a gente precisa achar onde o cisalhamento é máximo.
Vamos começar calculando as reações de apoio! Por isso, a melhor coisa a se fazer é um esboço do problema...
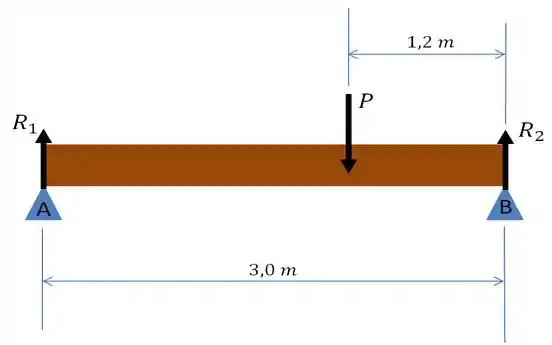
Do problema 5.1.9, sabemos que vale !
Aplicando as equações de equilíbrio:
Passo 2
O próximo passo agora é achar os gráficos de diagrama de esforço cortante e momento fletor...
Por isso analisemos seção por seção.
Comecemos analisando :
E depois :
O esforço cortante máximo, como podemos ver, vai se igual à !
Passo 3
Agora vamos determinar o momento de inércia!
Bem! Analisando a figura do enunciado, dá pra separar a seção transversal da nossa viga em dois retângulos, um onde o comprimento e a altura e outro onde e ...
Passo 4
Em seguida, vamos calcular o momento estático. Essa vai ser a parte mais complicadinha do exercício! Mas calma que vai dar bom!
Pra fazer isso, primeiro, precisamos determinar a posição da linha neutra dessa seção.
Para tanto, começamos separando a seção em elementos numerados e definindo uma posição na base da seção:
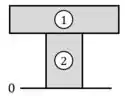
Em seguida, preenchemos em uma tabela os valores da área e da posição do centro de cada elemento:
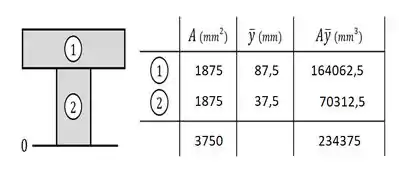
Ainda nessa tabela, também preenchemos na última coluna o produto desses valores para cada elemento e na última linha os somatórios e .
Com isso, podemos aplicar a fórmula:
E substituir os valores desses somatórios para encontrarmos a posição da nossa linha neutra:
Passo 5
O próximo passo, então, é identificar as fibras de interesse:
- As fibras no topo e na base da seção;
- As fibras onde ocorre uma mudança na largura da seção;
- E a fibra na linha neutra.
Fazendo isso, ficamos com o desenho abaixo:
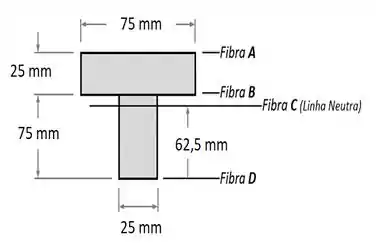
Sendo que nesse desenho, as dimensões foram adicionadas para já facilitar os cálculos do próximo passo.
Passo 6
Agora, devemos calcular os momentos estáticos .
Para as fibras e , podemos nos lembrar que os momentos estáticos das fibras no topo e na base de uma seção são iguais a zero, então:
Para a fibra , podemos escolher por observar a região acima dessa fibra.
Fazendo isso, vamos ter nessa região um único elemento retangular: o elemento que definimos anteriormente.
Esse elemento tem uma área e um centro com uma posição relativa à linha neutra .
Dessa forma, temos que:
Já para a fibra , é mais fácil escolher por observar a região abaixo dessa fibra.
Nessa região, vamos ter um único elemento retangular encostado na linha neutra com uma altura de e uma largura de .
Dessa forma, esse elemento vai ter uma área e um centro com uma posição relativa à linha neutra .
Sendo assim, temos:
Somando tudo, temos que...
Passo 7
Pra finalizar, aplicamos a equação do cisalhamento:
Onde é a largura da alma, no caso :
Bateu com o gabarito! Tamo indo bem, guys!