Um perfil soldado, tendo a seção reta mostrada como na figura , é fabricada com dois flanges de e uma alma de de espessura e de altura. Se a viga for sujeita à força cortante total de , qual força cada filete deve transmitir (por centímetro de comprimento de solda)?
Passo 1
Um torque é aplicado a um conjunto formado por dois eixos soldados.
Características do conjunto:
- Raio do eixo menor: . (Cilindro)
- Largura e altura da solda: e
- Inclinação da solda: .
Queremos saber a tensão média de cisalhamento que atua na na solda segundo a direção de (seção )
Como queremos a tensão somente onde em uma seção específica que não é concêntrica com os eixos (está inclinada!), só temos a fórmula original da tensão para nos ajudar:
A força aqui é alguma cortante que precisa balancear o torque . E a área vem do corte feito na solda. Vamos achar esses caras.
Primeiro, precisamos entender melhor o que está acontecendo nessa confusão toda.
Passo 2
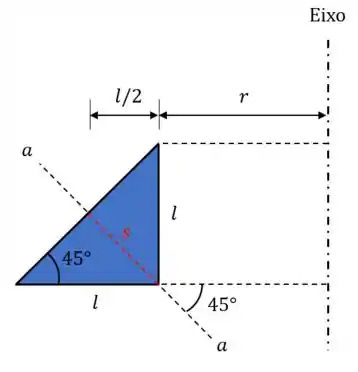
O torque promove uma torção do eixo menor ao redor do eixo dele (“Eixo” na figura). A solda mesmo só começa a uma distância desse eixo.
O corte que queremos passa na solda segundo a linha tracejada. Se você olhar na perspectiva da figura, o corte faz uma reta de comprimento na solda (linha tracejada vermelha).
Beleza, e daí? O que acontece é que a questão explica meio mal... A parte crítica da solda é a com a horizontal, mas você tem que pensar isso para solda inteira! Ou seja, pegue essa linha vermelha e gire ao redor do eixo!
A segunda figura deixa mais claro qual é a área em que a solda tem risco de falhar primeiro.
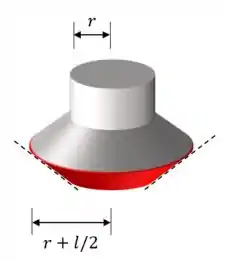
O vermelho dessa segunda figura é o que chamamos de uma superfície de revolução: porque a gente pegou aquele tracejado da primeira figura e giramos ao redor do eixo. Formou um tronco de cone. É nessa área aí que a tensão vai dar problema!
Para acharmos , precisamos dessa área vermelha!
Agora que organizamos o pensamento, vamos ver como fazer a conta pra área .
Passo 3
Então, existe uma fórmulinha pronta para a área superficial de um tronco de cone... mas ninguém sabe isso decorado... sério. Vale muito mais a pena você aprender uma parada nova pro seu arsenal: Primeiro Teorema de Pappus.
Funciona assim. Aquela reta de comprimento girou um ângulo de para gerar a figura a superfície vermelha. A área dessa superfície é
O é a distância do centroide da reta até o eixo. Calma que isso mole! A ideia é sempre essa: área é de uma superfície de revolução é o ângulo que girou vezes a posição do centroide vezes o tamanho da curva.
Beleza, o é fácil de achar. Na primeira figura do Passo , use o seno do ângulo
Agora a distância do centroide. O centroide é o centro geométrico da curva: para uma reta, é só o ponto no meio dele. Olha a figura seguinte.
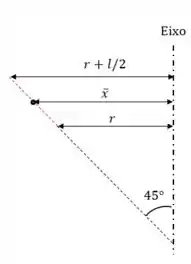
Como estamos tratando de de inclinação, vai ser a média dos outros valores, porque o centroide está bem no meio:
Aaah, finalmente vamos calcular essa área esquisita!
Beleza, agora precisamos só da força para achar a tensão .
Passo 4
Achar a força é mais tranquilo. O que está acontecendo é que a superfície vermelha na figura do Passo está girando. O resto do material resiste a esse giro com forças cortantes em cima da superfície!
Essas forças estão distribuídas ao longo da área. Mas como queremos calcular a tensão média, só estamos interessados em achar a força concentrada equivalente.
Essa força equivalente atua no centroide da reta de comprimento (então a uma distância do eixo) e tem que garantir o equilíbrio! Tem que equilibrar o efeito do torque . Então:
Passo 5
Boa, achamos todos os ingredientes. Só jogar na fórmula!