Enunciado
Mecânica dos Sólidos - Timoshenko - Mecânica dos sólidos - Vol 1- Ed: 1º - Capítulo 2.5 - Ex. 3
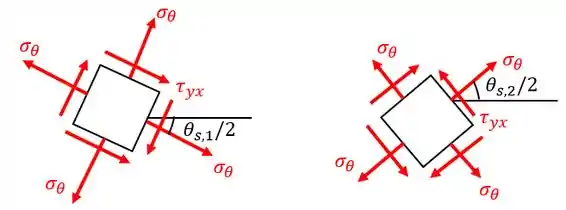
Determinar as tensões máximas de cisalhamento e os planos nos quais elas atuam para o elemento no problema anterior. Mostrar os resultados no desenho de um elemento.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Bom pessoal, temos que utilizar os dados da questão anterior, a 2.5.2, para determinar as tensões máximas de cisalhamento e os planos nos quais elas atuam.
Então, vamos começar determinando os planos de tensões máximas de cisalhamento (ângulo que devemos rotacionar o elemento para ter tensão cisalhante máxima). Portanto, temos:
Só que não esqueçam que são duas possíveis rotações, sendo ambos defasados de 90°! Então, temos e .
Passo 2
Agora que a gente conseguiu determinar os planos, vamos calcular as tensões.
Então, vamos começar pelas tensões normais. No estado de cisalhamento máximo, sempre teremos . Além disto, podemos afirmar que a soma das tensões normais sempre vai ser igual, independente da rotação do elemento. Isto é,
Já a tensão cisalhante máxima será:
E assim determinamos as tensões associadas a este estado!
Passo 3
Para finalizarmos a questão basta mostrarmos o resultado da rotação e das tensões esboçando o nosso elemento. Portanto, temos:
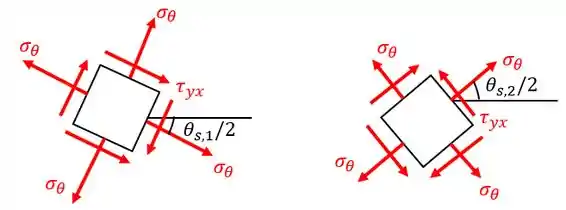
E assim finalizamos a questão!
Resposta
Os planos de máxima tensão cisalhante são: e .
As tensões associadas a este estado de tensão: e .
O esboço dos elementos são:
