Determine a tensão de cisalhamento máxima nas vigas verticais do problema 5.1.8
Passo 1
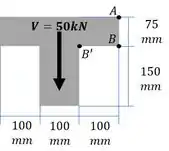
Dados da questão:
A questão pede: A distribuição de tensão sobre a viga.
Passo 2
Vamos começar calculando o centróide.
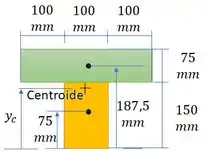
Passo 3
Agora calculamos o momento de inércia em relação ao centroide
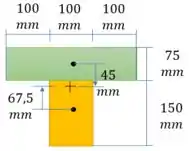
Passo 4
Agora vamos calcular o momento de inércia nos pontos de interesse.
O primeiro ponto de interesse é o ponto B e B’, por nesta região existe uma mudança bruca de espessura:
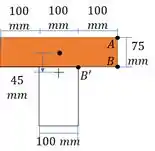
O segundo ponto de interesse é o ponto máximo. Este ponto pode ser calculado mais facilmente considerando toda a região abaixo do centroide.
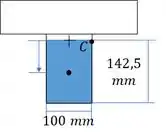
Passo 5
Agora basta aplicar a Equação 7.3 em cada ponto:
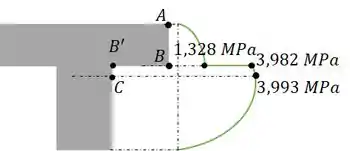
Tensão em :
Tensão em :
A tensão máxima:
Passo 6
Agora só desenhar a distribuição de tensão: