Uma viga de madeira simplesmente apoiada, de seção reta retangular (largura ), altura ), suporta uma carga concentrada , no meio do vão. Qual é o valor admissível de , sendo , e o vão .
Passo 1
Antes de tudo, vamos começar fazendo um esboço dessa viga e do que mais ou menos está acontecendo em nosso problema...
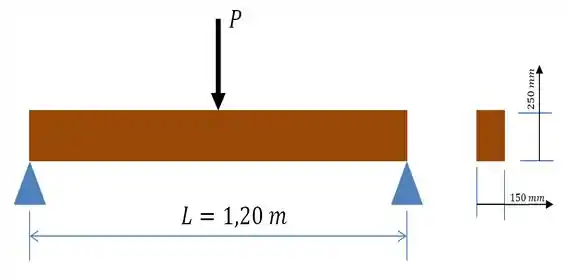
Bom! O que dá pra gente fazer de inicio, é calcular o momento polar de inércia da barra! O qual é dado por...
Passo 2
Feito isso, vamos analisar como se comporta o momento ao longo dessa nossa barra. Primeiro, bora fazer um esboço das forças atuantes...
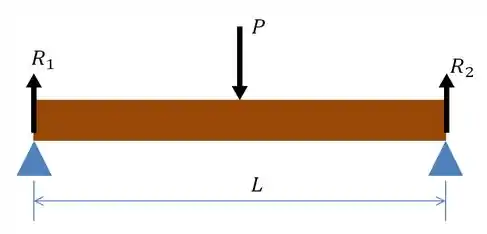
Como essas duas forças são simétricas, então...
Logo,
Assim, para qualquer ponto da barra que vai até a metade dela, o momento vai ser dado pela seguinte expressão...
E o momento máximo vai ocorrer em ...
Passo 3
O exercício nos deu o valor da tensão admissível !
Pois muito bem! A fórmula dela é dada por...
Como , então ficamos com...
Isolando e substituindo os valores numéricos...
Pronto! Conseguimos achar a nossa força admissível!