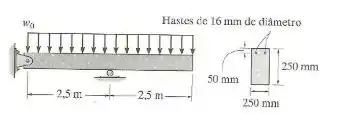
Qual deve ser a forma da viga em balanço mostrada na figura 5-25, de modo a obter-se um projeto completamente tracionado, se ela estiver sujeita a uma carga uniforme de intensidade , ao invés de uma carga concentrada? Considerar apenas as tensões normais devido à flexão, supondo que a tensão admissível seja
Passo 1
Faaaala, meu povo bonito!! Tudo bem com vocês?? A nossa questão de hoje nos traz uma viga composta por dois materiais diferentes, mas vou te explicar direitinho. Os materiais que compõem são o aço e o concreto, e ele nos pede para calcular a carga distribuída por toda a sua extensão, para uma tensão admissível dada. Viu?? Ela só tem cara de malvada, mas vamos resolver rapidinho. Vem comigo!!
Passo 2
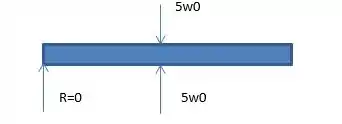
Nosso primeiro passinho de bebê vai ser achar as reações de apoio, a soma das forças e dos momentos.
![]()
![]()
Para
Para
Sabemos que o nosso sisteminha tem o momento máximo com . Então:
Agora que achamos a relação entre o nosso momento máximo e a carga distribuída, precisamos achar a relação entre os coeficientes e e a altura da nossa linha neutra.
Passo 3
Agora que já temos nossas dimensões, podemos calcular a nossa carga na viga. Para isso, vamos calcular primeiro o nosso I, para só depois substituir na nossa formulinha do momento.