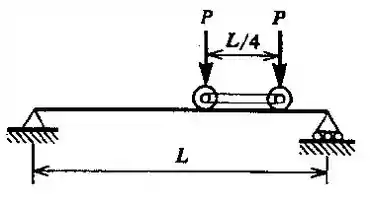
Duas rodas carregadas, com um afastamento , movem-se vagarosamente sobre uma viga simplesmente apoiada, de comprimento (ver a figura). Calculr o valor máximo de deflexão no vão da viga.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos determinar a máxima deflexão para a viga.
Esta deflexão irá ocorrer quando o centro do carrinho estiver exatamente no centro da viga. Assim, teremos um par de forças simétricas.
Só que para isto nós precisamos utilizar o método da superposição.
Passo 2
Então, utilizando o apêndice , temos a seguinte relação para a deflexão máxima para um par de forças simétricas:
Neste caso, a medida será:
Então, a deflexão máxima será:
E assim finalizamos a questão!