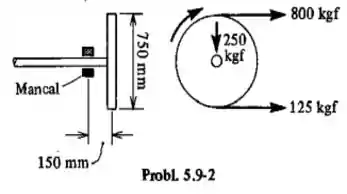
Um eixo de 65 mm de diâmetro suporta uma polia de de diâmetro pesando . As tensões na correia horizontal são e . Determinar a tensão principal de tração e a tensão máxima de cisalhamento no eixo do mancal, que está localizado a 150 mm da polia.
Passo 1
Primeiro, vamos determinar as tensões:
Logo, as tensões principais serão dadas por:
Substituindo os dados e fazendo a conta, teremos: