Um tubo cujo diâmetro externo mede e o momento de inércia polar , é suportado como se vê na Fig. 5-31ª. O torque aplicado é e a carga axial . Achar as tensões principais e a tensão máxima de cisalhamento no ponto , na superfície superior, supondo que a distância de à extremidade carregada da barra seja de .
Passo 1
Aqui, vamos primeira montar o diagrama de esforço cortante e momento fletor:
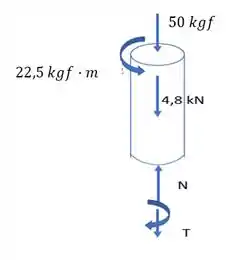
Agora é só realizar a análise dos esforços cortantes e momento fletor:
Passo 2
E agora, vamos realizar o cálculo da tensão de um ponto na superfície :
E em seguida, o cálculo da tensão máxima de cisalhamento de um ponto na nossa superfície:
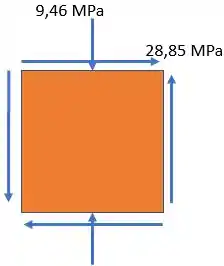
Passo 3
(a) Obtidas as tensões de estado plano já podemos calcular, então, as tensões principais; que são dadas pela fórmula abaixo:
Obtemos duas tensões, onde uma vai ser máxima, e outra vai ser mínima, .
Passo 4
(b) E por fim, vamos calcular a tensão de cisalhamento máxima no plano :
Resposta
(a) Tensões principais de um ponto na superfície :
(b) Tensão de cisalhamento máxima de um ponto na superfície :