Enunciado
Mecânica dos Sólidos - Timoshenko - Mecânica dos sólidos - Vol 1- Ed: 1º - Capítulo 2.2 - Ex. 5
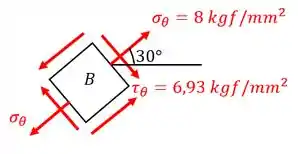
Um elemento em estado duplo de tensão é sujeito a tensões normais e (ver a Fig. 2.5). (a) Achar as tensões em um elemento girado de um ângulo . (b) Localizar os planos de tensão máxima de cisalhamento e determinar as tensões normal e de cisalhamento naqueles planos. (c) Localizar um plano no qual a tensão seja igual a zero; depois desenhar um elemento no qual este plano seja um lado e determinar as tensões normal e de cisalhamento em todos os lados do elemento.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Bom pessoal, temos muitas informações para determinar nesta questão. Então, vamos com muita calma responder cada uma das letras!
Começando pela letra a). Aqui temos que determinar as tensões em um elemento rotacionado de . Aqui é bem tranquilo, basta aplicarmos as fórmulas para as tensões normais e cisalhantes. Portanto,
Então, ao resolvermos o sistema acima, chegamos a seguinte resposta:
E assim nós finalizamos a letra a).
Passo 2
Agora vamos partir para a letra b). Aqui temos que determinar os planos de máxima tensão cisalhante e as tensões normal e cisalhante nesses planos.
Para obtermos esses planos, basta lembrarmos da seguinte relação:
Então, os planos de tensão cisalhante máxima são obtidos de uma rotação e . Agora, só nos resta calcularmos os valores das tensões. Substituindo o valor de nas mesmas relações utilizadas no Passo 1, obteremos:
Então, ao resolvermos o sistema acima, chegamos a seguinte resposta:
Passo 3
Para finalizarmos a questão, temos que resolver a letra c). Aqui temos que determinar um plano que possua uma tensão normal igual a zero e depois desenhar um elemento identificando estas tensões.
Para a nossa alegria, este plano foi encontrado lá no Passo 1! Quando , temos a tensão . E assim a gente já determinou o plano.
Por fim, esboçando o elemento identificando as tensões, temos:
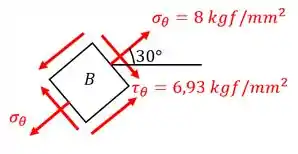
E assim finalizamos a questão!
Resposta
- Os planos de tensão cisalhante máxima são obtidos de uma rotação e . As tensões relativas a esses planos são:
- A tensão normal em um plano é igual a zero quando . O esboço do elemento é:
