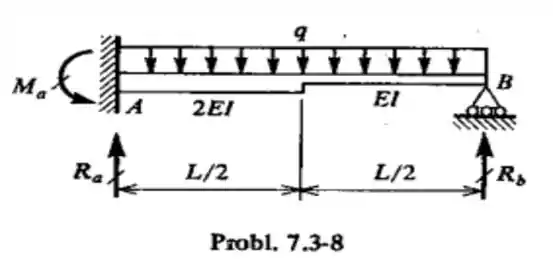
A figura representa uma viga não-prismática , com carga uniformemente distribuída. Calcular as reações.
Passo 1
Já vimos que para solucionar a nossa viga, precisamos resolver pelo método da superposição.
Por isso, vamos começar tornando !
Pois muito bem! A nossa viga não é prismática. Sabemos que de um trecho para outro temos uma relação de , sendo assim podemos afirmar que a força de reação em precisa ser o dobro da força de reação em ....
Passo 2
Como nossa viga não é prismática, vamos separas as deflexões geradas devido à ação da carga . De , temos que vai ser gerada uma deflexão igual à...
Já para o segundo trecho de , a deflexão gerada será de...
Somando as duas...
A deflexão devida a força de reação em pode ser obtida de acordo com o apêndice como sendo igual à soma nas duas partes....
Somando as duas...
E então, temos que...
Como...