Um fio longo está pendurado verticalmente e sujeito à ação do seu próprio peso. Calcular o maior comprimento que poderá ter sem causar rompimento se for de

aço e sendo a tensão de ruptura de .

alumínio, tendo tensão de ruptura de .

(Nota. O peso específico do aço é e o do alumínio , aproximadamente)

E aí meus querid@s, tudo bom com vocês? Simbora pra mais uma questãozinha?

Se liguem só, meus amigos. Primeiro de tudo vamos desenhar a situação retratada no problema de modo a facilitar nossa interpretação vamos imaginar a situação problema da seguinte forma, como se ilustra a seguir

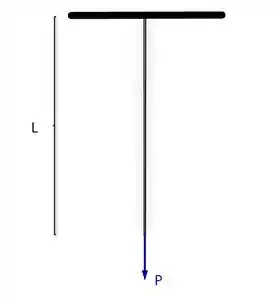
Foi nos fornecido a peso específico para cada uma das situações, devemos nos lembrar que essa propriedade do material pode ser descrita como sendo

Onde vai ser a carga que tá tracionando o fio e o volume do mesmo. Para esse caso, temos que o voluma será dado por , onde é a área de seção transversal e representa o comprimento do fio que é exatamente o que nós desejamos descobrir. Sendo assim, ficamos com a seguinte fórmula

Além disso, a questão também vai trabalhar com a tensão de ruptura que denotaremos aqui por e é dada por

Assim, substituindo ficamos com

E utilizaremos essa fórmula para resolver nosso problema, apenas adequando para o que é mencionado em cada alternativa.