Resolver o Probl. 2.1-7 usando o círculo de Mohr.

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

Bom pessoal, como precisamos resolver a questão 2.1-7 utilizando o círculo de Mohr, precisamos então começar a questão relembrando o problema.

Na questão nós temos um elemento rotaciono submetido as tensões e . Com estes valores, precisamos determinar as tensões , , e .

Infelizmente, com estes dois valores dados, é impossível construirmos o círculo de Mohr. Ou nós conhecemos por completo o estado rotacionado, isto é, os pontos e ou conhecemos o estado original e .

Então, para que a gente consiga esboçar o nosso círculo, vamos ter que calcular utilizando

as ferramentas lá da questão 2.1-7. Relembrando,

Para descobrirmos os outros valores, temos que calcular o ângulo . Ele é:

E então, temos:

Que, de uma certa forma, nós acabamos “resolvendo” a questão. Mas, como temos que fazer o círculo de Mohr, vamos para ele. A sua equação será:

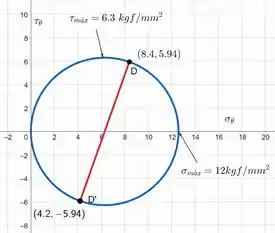
Esboçando o círculo com o estado inicial , temos:

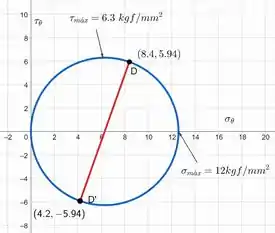
E assim finalizamos a questão!