Enunciado
Mecânica dos Sólidos - Timoshenko - Mecânica dos sólidos - Vol 1- Ed: 1º - Capítulo 2.4 - Ex. 2
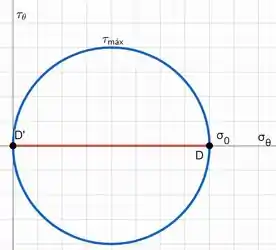
Desenhar o círculo de Mohr para o caso de tensão simples (ver a Fig. 2.4) e, a partir da geometria do círculo, verificar as Eq. (2-1), (2-2) e (2-3).
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos desenhar o círculo de Mohr para o caso de tensão simples e depois verificar algumas equações. Então, antes de escrevermos a equação do nosso círculo, vamos identificar quais as tensões no nosso elemento.
Como temos tensão de tração em uma única direção, temos e .
Substituindo estes valores na equação do círculo de Mohr, temos:
Esboçando o círculo, temos:
Passo 2
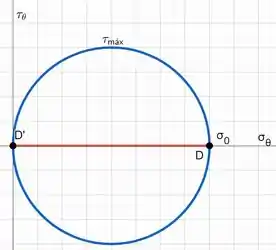
Agora temos que verificar as equações (2-1), (2-2) e (2-3). Através do círculo de Mohr.
Como o valor de tensão normal máximo é exatamente , então, temos que .
Já a tensão cisalhante máxima é exatamente o raio do círculo, e será dada por:
Agora só nos resta verificarmos as equações 2-1. Para fazermos isto, vamos ter que desenhar o círculo de Mohr indicando outro estado a partir de uma rotação . Sendo assim, teremos:
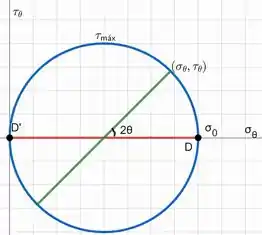
Como vocês podem ver, uma rotação no elemento significa uma rotação de no nosso círculo! Agora, é só expressarmos as tensões a partir de trigonometria. Logo,
E assim finalizamos a questão!
Resposta
