Resolver o Probl. 2.5-7 usando o círculo de Mohr.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Bom pessoal, como precisamos resolver a questão 2.5-7 utilizando o círculo de Mohr, precisamos então começar a questão relembrando o enunciado da questão.
Um elemento em estado plano de tensão é girado de um ângulo . No plano , as tensões são e . No plano , as tensões são e . Achar as tensões , e .
Então, a partir destes dois estados de tensão nós devemos obter o círculo de Mohr.
A sacada para esta questão está em perceber que para ambas as rotações é o mesmo valor! E, além dito, elas estão espaçadas de .
Então, qual é o único estado em que isto ocorre??? O estado de tensão de cisalhamento máximo! Ao percebermos isto, já podemos afirmar que e .
Agora é só partir para o círculo de Mohr!
Passo 2
Já passamos pelo mais difícil da questão. Agora é só aproveitar.
Então, vamos começar pelo círculo de Mohr. A sua equação será:
Esboçando o círculo com o estado inicial juntamente do estado do elemento após rotação temos:
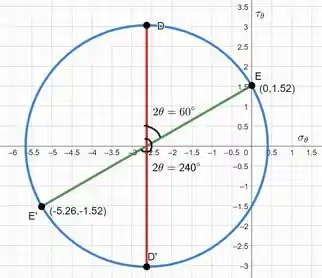
Como queremos obter as tensões , e do estado inicial, temos duas possibilidades: rotacionar o estado de tensão de cisalhamento máximo em ou , ambos no sentido anti-horário, como foi indicado no círculo de Mohr.
Então, ao rotacionarmos o estado de tensão de cisalhamento máximo e fizermos a interseção com o círculo, obteremos as seguintes tensões:
E assim finalizamos a questão!