Supondo que a viga representada na Fig 6-16 tenha seção transversal retangular com largura constante e altura variando linearmente de , em , até , em , calcular a deflexão em , quando
Passo 1
Galera essa questão é bem direta e pede para a gente achar a linha elástica. A gente só tem que achar primeiro o momento fletor antes e aplicar na equação da linha elástica:
Neste exercício é pedido apenas a equação linha estática à esquerda da força (perceba a direção de ).
Passo 2
Para achar o momento fletor primeiro precisamos achar as forças nos apoios, para isso vamos desenhar um esquema de forças.
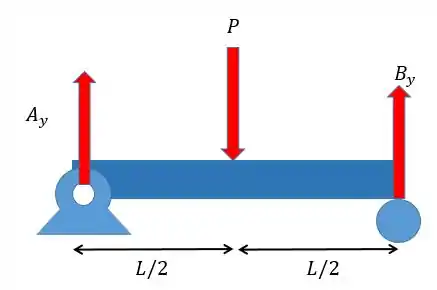
Pelas equações da estática vamos ter:
Para as forças em :
Pessoal, como se trata de um problema simétrico nem precisamos aplicar o somatório dos momentos já que as forças e serão iguais! Sendo assim,
Passo 3
Com as forças vamos poder achar o momento fletor, lembrando que precisamos apenas da metade esquerda. Logo, podemos desenhar o seguinte corte:
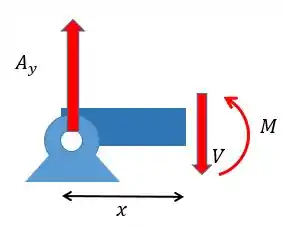
Fazendo o somatório das forças em de modo a achar a força cortante:
Agora podemos achar o momento fletor, fazendo o somatório dos momentos em torno do ponto e considerando o sentido horário positivo:
Uhulll achamos o momento!! Agora vamos achar a linha elástica!!
Passo 4
Para achar a linha elástica a gente só precisa daquela equação com uma derivada de segunda ordem:
Substituindo :
Agora vamos integrar em :
Mas pessoal, se liga na sacada mestre!!!
Como temos um problema simétrico, então no ponto central da viga vamos ter que , a inclinação, vale zero!!
Sendo assim podemos substituir na equação acima para achar :
Então temos:
E podemos integrar novamente para achar :
Agora vamos utilizar as condições de contorno para achar as contantes, olhando a nossa tabelinha a gente percebe que temos de utilizar as seguintes condições:
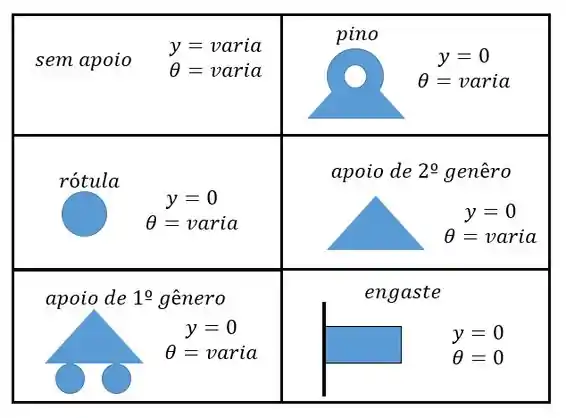
Como o pino se encontra em é só substituir e achar:
Logo,
Então a equação que temos é a seguinte:
Que pode ser expressa como:
Já temos a primeira parte do problema que é a linha elástica.
Passo 5
Agora vamos calcular a inclinação em , como a inclinação é dada pela equação:
É só substituir
A deflexão máxima ocorre no ponto central (pelo motivo de simetria) e vai ser dada por:
Substituindo