Enunciado
Mecânica dos Sólidos - Timoshenko - Mecânica dos sólidos - Vol 1- Ed: 1º - Capítulo 2.8 - Ex. 1
Usando as equações deduzidas no Art. 2.8, achar as deformações principais e e suas direções, se , e . Verificar os resultados por meio do círculo de Mohr para deformações.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Bom pessoal, esta é uma questão bem direta. Temos um estado plano de deformação e nós precisamos determinar as deformações principais e suas direções, seja através das equações como também através do círculo de Mohr.
A vantagem de ter esse trabalho dobrado é que a gente vai ter certeza do que estamos fazendo!
Então, vamos obter as deformações através das equações primeiramente. Relembrando, essas equações são:
Idêntica a equação para as tensões, não é? Então, substituindo os valores, teremos:
E com isto chegamos as deformações principais e .
Passo 2
Para finalizarmos a primeira parte da questão (resolver através das equações), precisamos encontrar as direções de máxima deformação.
Sendo assim, temos:
Só que não esqueçam que são duas possíveis rotações, sendo ambos defasados de 90°! Então, temos e
E assim a gente determinou todas as informações que a questão pediu, só que através das equações.
Passo 3
Agora nós precisamos determinar as mesmas informações que vimos nos Passos 1 e 2, só que através do círculo de Mohr para deformação.
Sendo assim, vamos começar determinando a equação deste círculo. Ela será:
Sendo e . Portanto,
Esboçando o círculo com o estado inicial juntamente do estado do elemento após rotação temos:
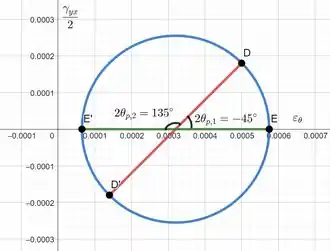
Ao encontrarmos a interseção da reta rotacionada (eixo x) com o círculo teremos as nossas deformações principais. Neste caso, elas serão:
E as direções são: e .
Resposta
As deformações principais são e . Já as direções são e .