Uma viga em balanço, afilada, de seção reta retangular, é sujeitas as cargas mostradas na figura. A largura da viga é constante e igual a , enquanto a altura varia linearmente de na extremidade carregada, a no apoio. Calcular a tensão normal máxima devido á flexão
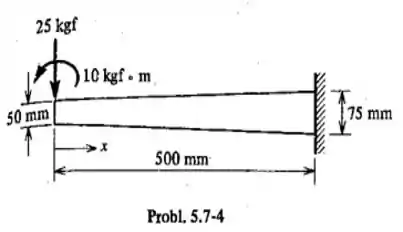
Passo 1
Dados da questão: , e
Para resolver a questão precisamos aplicar a equação da flexão. Porém, o momento interno e a geometria da seção mudam com a distância. Então faremos o seguinte procedimento:
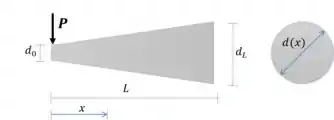
- Encontramos uma equação para o momento fletor
- Encontramos uma equação para o momento de inércia
- Aplicamos a equação da flexão
- Derivamos e igualamos a equação da flexão a zero para encontrar o ponto de máximo
- Utilizamos o valor encontrado para determinar a tensão máxima
Passo 2
Vamos começar calculando uma equação para o momento fletor. Note que não é preciso calcular as reações de apoio.
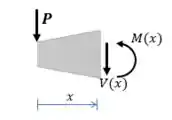
Passo 3
Vamos investigar o comportamento do diâmetro ao longo da seção
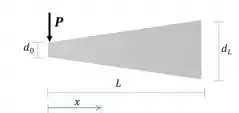
O comportamento é linear:
As condições de contorno são:
Resolvendo termos:
A equação final é:
Passo 4
Agora vamos determinar expressões que representem as propriedades geométricas:
Passo 5
Vamos aplicar na fórmula da flexão
Substituindo
Simplificando
Passo 6
Agora vamos derivar a equação para encontrar o ponto de máximo:
Pondo em evidência:
Chegamos em:
Daqui temos duas opções:
- , o valor negativo não é possível!
- , vamos ficar com essa função
Então, vamos aplicar os valores:
Passo 7
Vamos aplicar o valor de na equação da tensão:
Aplicando os valores: