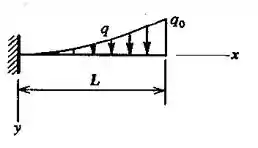
Uma viga em balanço suporta uma carga parabólico, como se vê na figura. Sendo a taxa de carregamento , calcular a inclinação máxima da viga.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos determinar a inclinação máxima da viga submetida a um carregamento parabólico.
Para resolvermos esta questão utilizando o método de superposição, nós precisamos substituir o carregamento parabólico. Precisamos fazer isto pois, para nós não temos nenhuma relação equivalente no apêndice para podermos utilizar.
Então, vamos substituir o carregamento parabólico por várias cargas pontuais forças . Lá do apêndice , nós temos que a deflexão em uma viga em balanço para uma concentrada que dista da extremidade esquerda é:
Então, se o é a distância até a carga concentrada, temos:
Só que nós temos “infinitas” forças pontuais . Então, se somarmos todas elas (o que significa integrar a nossa função, teremos:
E agora basta resolvermos esta integral!
Passo 2
Para podermos resolver a integral, temos que escrever a função para o carregamento . Como já foi dado no enunciado da questão, temos .
Sendo assim teremos a seguinte integral:
Agora só nos resta desenvolvermos ela. Portanto,
E assim finalizamos a questão!