Para a viga representada na Fig 7-6a, selecionando como redundante, calcular todas as reações e traçar os diagramas de força cortante e momento fletor.
Passo 1
Bora lá, guys! Da figura 7-6a...
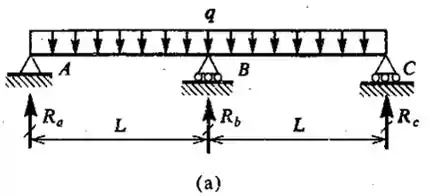
Extraímos que...
Logo...
A expressão geral do momento fletor, então, é dada por...
Para a seção de até :
Para a seção de até :
E fazendo o cálculo do esforço cortante...
Para a seção de até :
Para a seção de até :
Passo 2
Assim, conseguimos plotar os gráficos abaixo... Para um e um , fixando o valor de em , temos o seguinte gráfico de momento fletor:
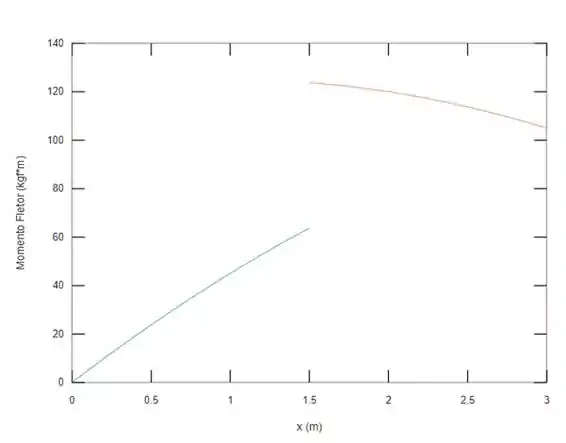
E de esforço cortante:
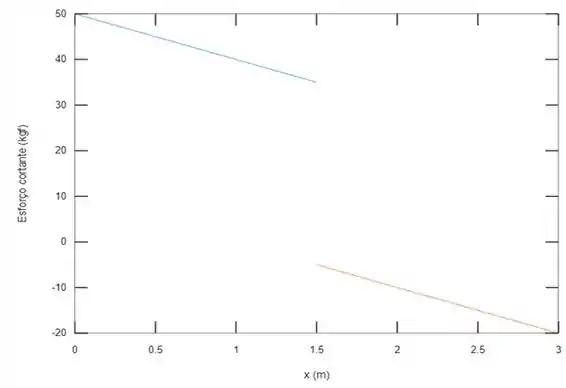
Resposta
Ei, a resposta está no passo a passo :)