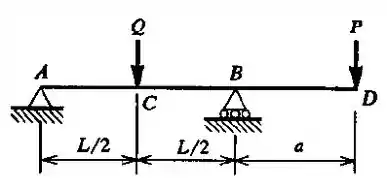
Para a viga representada na figura, achar a relação tal que a deflexão sob a carga seja nula.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos calcular a relação tal que a deflexão em seja nula.
Para isto, vamos utilizar o mesmo raciocínio desenvolvido na questão 6.5-11. A deflexão em será dada exatamente por:
Sendo a inclinação da viga em e a deflexão de se nós imaginarmos que a viga está em balanço com uma carga na extremidade livre.
Bom, agora que a gente já sabe o que fazer, vamos calcular a inclinação em .
Passo 2
Para calcularmos a inclinação em será necessário converter a carga pontual em uma carga e momento que atuam em .
A força equivalente que atua em possui a mesma intensidade da força que atual em . Portanto,
Já o momento fletor deverá ser igual a:
Agora já sabemos os esforços que atuam na viga !
Passo 3
Agora já podemos calcular o deslocamento angular em . Para isto, basta lembrarmos que:
Relembrando, como a força está exatamente em cima do vínculo , ele não afeta no deslocamento angular e nem na deflexão da viga .
Então, utilizando as relações do apêndice nós temos:
E assim nós temos o deslocamento angular em .
Passo 4
Para finalizarmos a questão, só nos resta desenvolvermos a equação do Passo 1. Portanto,
E assim finalizamos a questão.