A viga está sujeita a cargas uniformemente distribuídas de intensidade e , como mostrado na figura. Achar a força cortante e o momento fletor no ponto e também no meio da viga. Admitir ; e .
Passo 1
O problema quer que a gente encontre o esforço cortante e o momento fletor na viga. Vamos começar calculando a carga , para depois fazer um diagrama de corpo livre diagraminha de corpo livre, vamos lá usando o equilíbrio de forças:
Então, o diagrama fica assim:
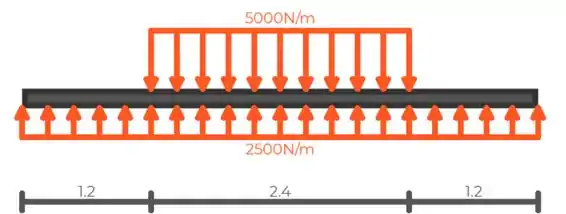
Passo 2
Então devemos encontrar o esforço cortante em :
Onde o , a gente pode encontrar o efeito cortante:
Passo 3
Agora, o momento fletor em :
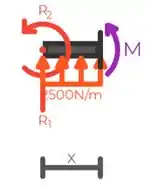
Onde o , a gente pode encontrar o momento fletor:
Passo 4
Por fim, calculamos o mesmo para o meio da viga, primeiro o efeito cortante:
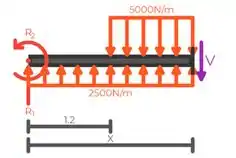
Onde , que é o meio da viga.
E o momento fletor:
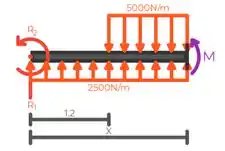
Onde , que é o meio da viga.