Três rodas movem-se através de uma viga simplesmente apoiada, como é mostrado na figura. Determinar a posição das rodas, segundos a distância , de modo a produzir o momento fletor máximo na viga, admitindo que e . Determinar também o momento fletor máximo.
Passo 1
Bom galera, Vamos começar com um diagraminha de corpo livre, que fica assim:
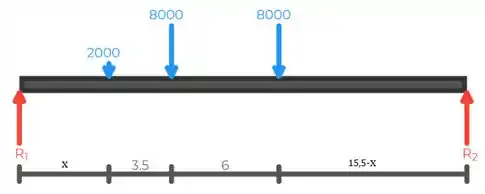
Passo 2
Belezinha, vamos usar o equilíbrio de forças, bora lá:
Agora vamos pra o momento, usando como eixo de rotação:
A partir disso temos:
Passo 3
Show de bola, o problema pede qual deve ocorrer o maior momento fletor, a gente sabe que é o que ocorre entre as duas cargas de , então vamos calcular o momento fletor na segunda carga , vamos lá:
Temos a expressão que representa o momento fletor na segunda carga , para encontrarmos em que valor , teremos o momento fletor máximo, devemos derivala e igualamos a , e ficamos com:
Então, o nosso momento fletor máximo ocorrerá quando e será: