Achar as reações e da barra estaticamente indeterminada da Fig 1-11a, tornando como redundante.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
A questão nos pede para determinarmos as reações e . Mas, para isto, vamos começar relembrando a Figura 1-11a abaixo.
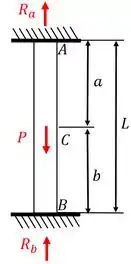
Para tornarmos a reação redundante, devemos retirar o apoio da barra neste ponto e mantermos a força . Ao fazermos isto, temos a seguinte estrutura livre:
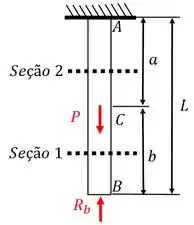
Agora é só repetirmos o que fizemos em outras questões semelhantes. Como sabemos que a barra não se deforma, a soma das deformações de cada seção deverá ser igual a zero. Logo, para obtermos a nossa primeira reação, basta fazermos:
Já a nossa segunda reação virá da equação da estática! Como a barra está em equilíbrio, o somatório de forças é nulo. Logo,
E assim obteremos a nossa segunda reação!
Agora que já sabemos tudo, vamos aos cálculos!
Passo 2
Vamos começar pela seção 1, indicada na figura do Passo 1. Desenhando o diagrama de equilíbrio, temos:
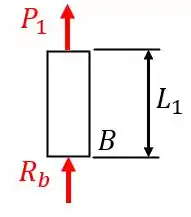
Portanto, como a barra está em equilíbrio , então, a força é igual a e a deformação devido a esta seção será:
Agora, basta repetirmos para a seção 2! Esboçando o diagrama de equilíbrio para a seção 2, temos:
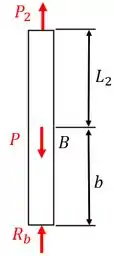
Para a seção 2, aplicando a relação de equilíbrio, obtemos . Portanto, a deformação devido a esta seção será:
Passo 3
Agora que determinamos as deformações de cada seção da barra, vamos utilizar a condição de não deformação da barra. Sendo assim, temos:
E assim descobrimos a nossa primeira reação!
Passo 4
Para finalizarmos a questão, basta somarmos utilizarmos a relação da estática obtida no Passo 1. Como o somatório de forças na direção vertical é igual a zero, temos:
E assim finalizamos a questão!