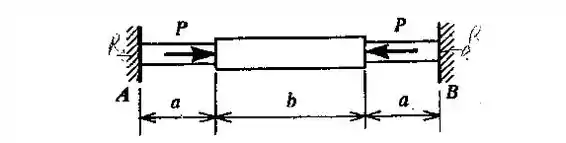
Uma barra tem seção reduzida nas extremidades, como se vê na figura, está engastada em suportes rígidos, e suporta forças axiais e opostas, . Calcular a tensão no meio da barra, supondo área da seção transversal nas extremidades e área da seção transversal na parte central. (Usar os seguintes valores numéricos: ; ; ; .).
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Nesta questão temos que calcular a tensão no meio da barra. Então, para que possamos fazer isto, temos que determinar quem é a força atuante nesta seção.
Só que teremos um trabalhinho na frente. Aqui temos uma estrutura estaticamente indeterminada devido as duas paredes nas suas extremidades.
O procedimento para resolvermos esta questão será bem semelhante a questão 1.6-1. Vamos substituir a parede em por uma reação , conforme pode ser visto abaixo:
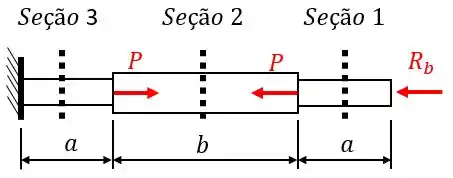
Depois, vamos determinar esta reação de tal forma que a estrutura não se deforma . Ao calcularmos o valor desta reação, conseguiremos obter a força no meio da barra e consequentemente a tensão.
Agora que já sabemos tudo, vamos aos cálculos!
Passo 2
Agora devemos calcular as deformações de cada seção. Vamos começar pela seção 1, indicada na figura do Passo 1. Desenhando o diagrama de equilíbrio, temos:
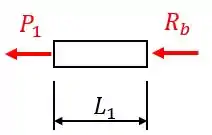
Portanto, como a barra está em equilíbrio , então, a força é igual a e a deformação devido a esta seção será:
Agora vamos repetir o procedimento anterior, só que para a seção 2! Esboçando o diagrama de equilíbrio para a seção 2, temos:
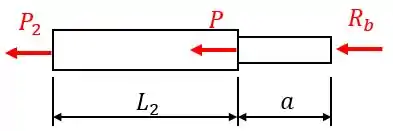
Para a seção 2, aplicando a relação de equilíbrio, obtemos . Portanto, a deformação devido a esta seção será:
Agora para a seção 3, temos o seguinte diagrama de corpo livre:
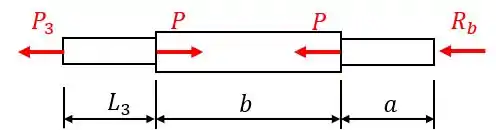
Aplicando a relação de equilíbrio, obtemos . Portanto, a deformação devido a esta seção será:
E assim terminamos de calcular a deformação de todas as seções!
Passo 3
Agora já temos informações suficientes para calcularmos a reação . Como dissemos no Passo 1, a deformação total da barra é nula. Utilizando então esta condição, temos:
Como a força é igual a , temos:
Passo 4
Após determinarmos já finalizamos a questão??
Não! Lembrando, o que queremos é a tensão no meio da barra! Nós calculamos pois, como pode ser visto no Passo 2, a força no meio da barra é:
Logo, a força dependia de ! Substituindo os valores que obtivemos, temos:
Calculando a tensão, temos:
Uma tensão de compressão! E assim finalizamos a questão!