Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica dos Sólidos - Timoshenko - Mecânica dos sólidos - Vol 1- Ed: 1º - Capítulo 5.7 - Ex. 1

Achar a tensão normal máxima devido á flexão para a viga em balanço mostrada na F i g   5 - 24 , sendo d b d a = 3 . Comparar esta tensão com a tensão máxima, σ b , no apoio.

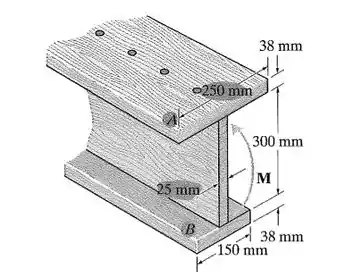
Passo 1

O problema nos pede para calcularmos a tensão normal de flexão   σ , descrita por:

σ = - M y I Onde:

M é o momento fletor aplicado na seção transversal;

y é a posição onde se quer calcular a tensão de flexão σ em relação à linha neutra da viga;

I é o momento de inércia da área da seção transversal da viga em relação à sua linha neutra.

Passo 2

Então vamos começar determinando a posição y da linha neutra. Para isso, devemos numerar as três tábuas da viga e identificar a sua base como a posição 0:

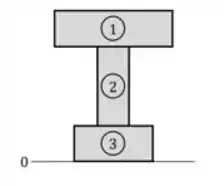
Depois, devemos fazer uma média das posições y i -   dos centros de cada tábua ponderada de acordo com cada área A i . Fica assim:

y - = ∑ A i y - i ∑ A i

y - = 4909,8 × 10 3   m m 3 22700   m m 2

y - = 216,3   m m

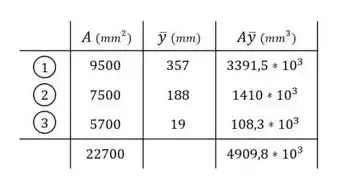
Passo 3

Vamos agora calcular o momento de inércia I da viga. Para isso, devemos calcular o momento de inércia I i para a área cada tábua da nossa viga. Sabemos que I i é dado por:

I i = b h 3 12

Para I 1 , temos uma base b = 250   m m e uma altura h = 38   m m , logo:

I 1 = 250 × 38 3 12 = 1143167   m m 4

Para I 2 , temos uma base b = 25   m m e uma altura h = 300   m m , logo:

I 2 = 25 × 300 3 12 = 56250000   m m 4

Para I 3 , temos uma base b = 150   m m e uma altura h = 38   m m , logo:

I 3 = 150 × 38 3 12 = 685900   m m 4

Em seguida, temos que cada tábua tem uma distância d i entre o seu centro e a linha neutra da viga:

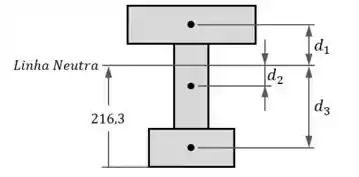
Visto que cada tábua tem um centro, sendo o centro de 1 →   h = 357   m m , 2 → h = 188   m m   e 3 → h = 19   m m   . Vamos calcular a d i de cada uma:

d 1 = 357 - 216,3 = 140,7   m m d 2 = 216,3 - 188 = 28,3   m m d 3 = 216,3 - 19 = 197,3   m m

Agora, temos que o momento de inércia I da viga é dado por:

I = ∑ I i + A i d i 2 I = ( 1143167 + 9500 × 140,7 2 + ( 56250000 + 7500 × 28,3 2 + ( 685900 + 5700 × 197,3 2 ) I = 474,04 × 10 6   m m 4

Passo 4

Por fim, basta substituirmos os dados encontrados na fórmula da tensão de flexão:

σ m á x = - M y m á x I

σ m á x = - 1,5   k N . m - 216,3   m m 474,04 × 10 6   m m 4

σ m á x = 0,684   M P a

Passo 5

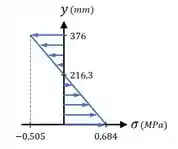
Agora, falta esboçarmos a vista 3 D . Para isso, precisamos calcular a tensão de flexão no topo da viga.

σ t o p o = - M y t o p o I

O y t o p o é dado por:

y t o p o = 38 + 300 + 38 - 216,3 = 159,7   m m

y t o p o = - 1,5   k N . m 159,3   m m 474,04 × 10 6   m m 4

y t o p o = - 0505   M P a

Com isso, considerando um eixo y começando na base da viga, podemos marcar os pontos:

  • σ = 0,684   M p a para a base da viga, onde y = 0 ;
  • σ = 0 para a linha neutra, onde y = y - = 216,3 m m ;
  • σ = - 0,505   M p a   para o topo da viga, onde   y = 38 + 300 + 38 = 376   m m

Com esses pontos, temos que:

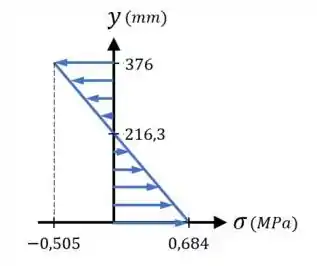
Resposta

σ m á x = 0,684   M P a

Ver Outros Exercícios desse livro