Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica dos Sólidos - Timoshenko - Mecânica dos sólidos - Vol 1- Ed: 1º - Capítulo 5.9 - Ex. 6

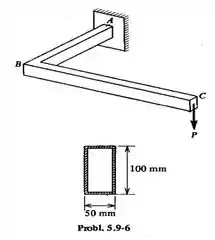
Um suporte em forma de L disposto num plano horizontal, suporta uma carga P = 180   k g f . O suporte tem uma seção retangular, vazada, medindo extremamente 50   m m × 100   m m . A espessura da parede é 2   m m . O comprimento do braço A B é 250   m m e do braço B C , 500   m m . Achar as tensões principais no ponto A localizado no topo do suporte, no apoio.

Passo 1

Primeiro, vamos determinar as tensões:

σ x =

τ = T c J = ( 180 ) × 0,05 1 12 50 100 3 - 1 12 46 96 3 = 0,76   k g f / m m 2

σ y = ( 180 ) 50 100 - 46 96

Logo, as tensões principais serão dadas por:

σ 1,2 = σ x + σ y 2 ± σ x - σ y 2 2 + τ x y 2

σ 1,2 = 1,27   k g f / m m 2 2 ± 1,27   k g f / m m 2 2 2 + 0,76   k g f / m m 2 2

Substituindo os dados e fazendo a conta, teremos:

σ 1 = 1,6   k g f / m m 2

σ 2 = - 0,003   k g f / m m 2

Resposta

σ 1 = 6,45   k g f / m m 2

σ 2 = - 3 , 55   k g f / m m 2

Ver Outros Exercícios desse livro