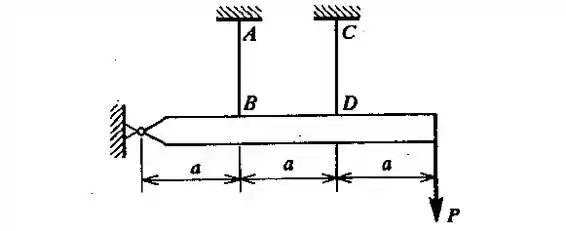
Achar as tensões nos dois cabos idênticos e (ver a figura), de área de seção transversal , admitindo que a barra horizontal seja rígida. (Supor e ).
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
O objetivo desta questão é obter as tensões nos dois cabos, admitindo que a barra seja rígida.
Temos aqui um problema estaticamente indeterminado (4 incógnitas e três equações de equilíbrio). As incógnitas são: 1 para cada cabo e 2 devido ao suporte lateral que prende a barra horizontal a parede.
Para este tipo de questão, precisamos trabalhar tanto com as equações de equilíbrio da estática quanto as de deformação. Portanto, vamos começar pela mais fácil, que é o diagrama equilíbrio.
Se substituirmos estes vínculos pelas forças, teremos o seguinte diagrama de equilíbrio:
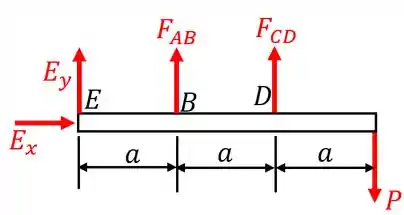
Aplicando as equações da estática, ao fazermos o somatório de momentos em torno do ponto , temos:
Precisamos apenas de uma outra equação que correlacione as forças e para que possamos montar um sistema e obter as forças de cada uma!
Passo 2
Agora temos que descobrir outra equação para que possamos montar o nosso sistema.
Como dissemos no Passo 1, agora precisamos trabalhar com a deformação da barra.
Pelo fato da barra ser rígida, sabemos que ela não se deforma. Portanto, as deformações dos cabos em e devem ser proporcionais com a geometria da barra de forma que ela continue reta.
E esta proporcionalidade é a nossa chave. Aplicando esta relação, teremos a seguinte relação de triângulos:
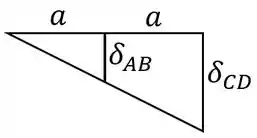
Portanto, temos que:
Substituindo a fórmula da deformação de cada cabo na relação acima, obtemos:
Mas como , e , temos:
E assim conseguimos a nossa relação!
Passo 3
Juntando as informações que conseguimos nos dois últimos Passos, temos o seguinte sistema:
Resolvendo o sistema acima obtemos e .
Então, para finalizarmos a questão, só nos resta calcularmos as tensões em cada cabo. Portanto,
E assim finalizamos a questão!