Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica dos Sólidos - Timoshenko - Mecânica dos sólidos - Vol 1- Ed: 1º - Capítulo 1.5 - Ex. 7

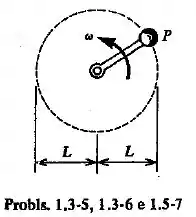
Uma barra de comprimento L gira em um plano horizontal, em torno de um eixo vertical, com velocidade angular ω (ver a Fig. Probl. 1.3-5). A área da seção transversal da barra é A e o peso da barra é P 1 . Um peso P é preso à extremidade da barra. Calcular o alongamento, δ , decorrente da força centrífuga.

Passo 1

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

Bom pessoal, esta questão é basicamente uma continuação da questão 1.3-6. Vamos precisar utilizar bastante as informações que lá descobrimos.

Na questão 1.3-6 nós determinamos uma força F p = P ω 2 L g na extremidade da barra e uma força F b = γ A L 2 ω 2 2 g   no centro dela. Portanto, temos duas seções com forças distintas que se deformarão.

A diferença nesta questão é que lá na questão 1.3-6 nós não tínhamos o peso da barra. Já nesta questão, nós sabemos que ele é P 1 . Esta pequena mudança vai mudar apenas a relação da força centrífuga que aqui utilizaremos, a qual será agora:

F b = m b ω 2 R = P 1 g ω 2 L 2 = P 1 L ω 2 2 g

Continuando, a nossa resposta final será exatamente a soma das deformações de ambas as seções. Por isto, vamos determinar cada uma delas agora!

Passo 2

Vamos começar determinando a seção que está sujeita apenas a força F b = P ω 2 L g . A sua deformação será:

δ 1 = F p L 1 E A = P ω 2 L g L 2 E A

δ 1 = P ω 2 L 2 2 g E A

Já a outra seção está sujeita a força F p + F b . Portanto, a sua deformação será:

δ 2 = F p + F b L 2 E A = P ω 2 L g + P 1 L ω 2 2 g L 2 E A

δ 2 = P ω 2 L 2 2 g E A + P 1 L 2 ω 2 4 g E A

Passo 3

Para finalizarmos a questão, basta somarmos o que obtemos. Portanto, o alongamento da barra será:

δ = δ 1 + δ 2

δ = P ω 2 L 2 2 g E A + P ω 2 L 2 2 g E A + P 1 L 2 ω 2 4 g E A

δ = ω 2 L 2 g E A P + P 1 4

E assim finalizamos a questão!

Resposta

δ = ω 2 L 2 g E A P + P 1 4

Ver Outros Exercícios desse livro