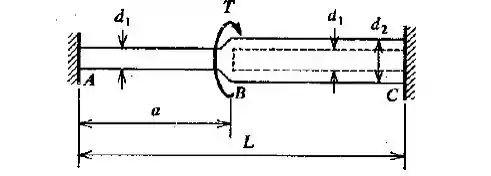
Uma barra, , engastada em ambas as extremidades é sujeita a um torque, , na seção (ver a figura). A barra é circular com diâmetros , de a e diâmetro externo = , diâmetro interno = de a . Deduzir uma expressão para a razão , de maneira que os torques reativos em e sejam numericamente iguais.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
A primeira parte da questão consiste em entender o que está acontecendo e as forças ao qual a nossa barra está submetida.
Então, temos aqui um problema estaticamente indeterminado. Devido a presença dos dois engastamentos, teremos torques e para impedir o movimento das extremidades das barras.
Estes dois torques são tais que:
E, como foi dito pelo enunciado da questão, eles são numericamente iguais. Logo,
Passo 2
Agora que já obtivemos uma relação para os torques, precisamos trabalhar com a barra para obter a relação que a questão pede.
Como a barra está estaticamente indeterminada, precisamos substituir algum dos apoios pelo torque que a reação exerce.
Então, vamos substituir o apoio em pelo torque , como podemos ver abaixo:
Mas, como o ângulo de rotação em deve ser nulo, temos:
Agora é só substituirmos os termos acima pelos seus valores corretos (momentos de inércia para eixo vazado ou não e o torque entre cada seção). Portanto,
E assim a gente finaliza a questão!