Enunciado
Mecânica dos Sólidos - Timoshenko - Mecânica dos sólidos - Vol 1- Ed: 1º - Capítulo 2.1 - Ex. 3
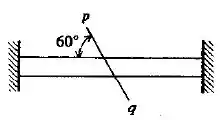
Uma barra de metal se encaixa entre dois suportes rígidos, à temperatura ambiente , como se vê na figura. Calcular as tensões normal e de cisalhamento na seção inclinada, quando a temperatura aumenta para 95 °C. Admitir por °C e .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta é uma questão que temos que dividir em duas partes. Primeiro vamos descobrir qual é a força compressiva que surge devido a dilatação térmica da barra, afinal, o comprimento deve ser mantido constante.
Depois, a segunda parte e o objetivo da questão, é descobrir qual a tensão normal e de cisalhamento na seção inclinada .
Então, vamos começar calculando quem é a força compressiva. Esta força deve ter intensidade tal que a deformação devido a compressão seja exatamente igual a deformação devido a dilatação. Portanto,
Passo 2
No final do Passo 1 nós descobrimos que surgirá uma tensão compressiva igual a na direção axial da barra.
Agora, só nos resta calcularmos as tensões na superfície inclinada. Para isto, vamos definir o ângulo formado entre a seção e a vertical. Esse ângulo será dado por:
Com posse deste ângulo , utilizando as relações já desenvolvidas na seção 2.1 do livro, teremos:
E assim finalizamos a questão!