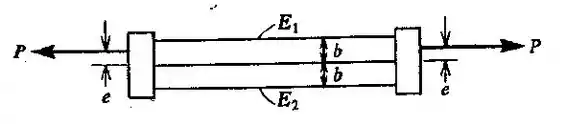
Uma barra de seção quadrada é formada por duas outras de materiais diferentes, tendo os módulos de elasticidade e (ver a figura). As seções transversais das barras são iguais. Supondo que as placas das extremidades sejam rígidas, estabelecer a fórmula para o cálculo da excentricidade, , de modo que ambas as barras tenham a mesma tensão. (Nota: Supor .).
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Vamos primeiro descrever um pequeno problema da questão. Se as duas barras, que possuem a mesma seção transversal, devem possuir a mesma tensão, as forças submetidas a elas devem ser iguais entre si. Além disto, elas devem ser iguais a . E isto tudo independe da excentricidade !
Portanto, a questão possui um erro de escrita! O mais provável é que fosse desejado que as barras possuíssem a mesma deformação (e é assim que iremos trabalhar aqui agora).
Então, vamos obter a equação para a excentricidade tal que as duas barras tenham a mesma deformação.
Só que nós não conhecemos nada ainda da estrutura. Isto é, não sabemos quem são as forças em cada barra e muito menos a distância (três incógnitas).
Para este tipo de questão, precisamos trabalhar tanto com as equações de equilíbrio da estática quanto as de deformação. Portanto, vamos começar pela mais fácil, a mais intuitiva.
Em outras palavras, vamos começar pela deformação! Se a barra é mantida na posição horizontal, então a deformação de ambos os fios é igual! Desenvolvendo esta relação, temos:
Como eles tem mesmo comprimento e área, temos:
Passo 2
Agora que já trabalhamos com a deformação, precisamos trabalhar com a equação de equilíbrio da estática. Ao fazermos isto, obteremos uma segunda equação que possibilitará com que resolvamos o nosso impasse (quem é a distância ).
Antes de aplicarmos as relações, temos que substituir a barras por reações. Ao fazermos isto, teremos o seguinte diagrama de corpo livre:
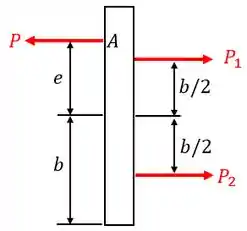
Agora, basta aplicarmos as equações de equilíbrio. Portanto:
Passo 3
Para finalizarmos a questão, basta juntarmos as duas equações obtidas no Passo 2 com a equação obtida no Passo 1.
Ao fazermos isto, chegamos a um sistema de 3 equações, conforme pode ser visto abaixo:
Como nosso objetivo é apenas a distância , basta substituirmos a primeira equação na terceira. Ao fazermos isto, temos:
E assim finalizamos a questão!