Considerando o sistema representado na Fig. 1-15a, estabelecer a fórmula para calcular o acréscimo de temperatura, , que fará com que toda a carga seja carregada pelo tubo de cobre. (Fazer e representar os coeficientes de dilatação linear, módulos de elasticidade e áreas das seções transversais para o aço e cobre, respectivamente.).
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta questão é uma modificação do Exemplo 3 resolvido durante o capítulo. Portanto, vamos aqui utilizar algumas ideias lá desenvolvidas.
Mas, antes disto, vamos relembrar a geometria da questão abaixo:
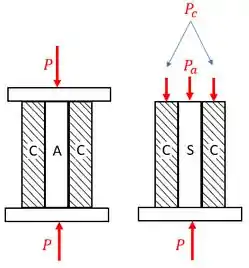
A partir desta geometria, temos que descobrir qual o acréscimo de temperatura que fará com que a carga seja toda concentrada no tudo de cobre. Portanto, e , sendo as cargas no aço e no cobre respectivamente.
Passo 2
Para darmos continuidade a questão, é fundamental que a gente entenda o que está acontecendo. Portanto, vamos primeiro entender o porquê disto acontecer.
Como o cobre tem um coeficiente de dilatação maior que o aço, ele irá aumentar de comprimento mais rapidamente que o aço.
Aos poucos, isto fará com que a tensão na barra diminua, pois a mesma não deve ser deformada tanto para que atinja a mesma dimensão que a barra de cobre.
Mas isto ocorrerá até um caso limite, em que a deformação térmica da barra de cobre, somada com a deformação devido a ação da força seja exatamente igual a deformação térmica do aço. Nesta condição, a força no aço será nula!
Escrevendo o texto anterior em forma de equação, temos:
Agora é só substituirmos com as relações de cada deformação. Portanto,
E assim finalizamos a questão!