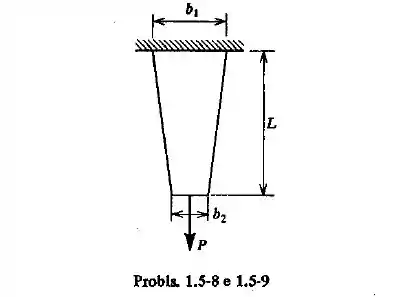
Uma barra de seção transversal retangular, variável, com espessura, e, constante, suporta uma força , como se vê na figura. A largura da barra varia linearmente de , no suporte, até na extremidade livre. Estabelecer a fórmula para o cálculo do alongamento, , da barra devido a ação de .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Este é um tipo de questão que costuma assustar bastante! Por estarmos trabalhando com uma barra de seção transversal variável, não podemos utilizar as relações para o alongamento já deduzidas do livro.
Infelizmente nós temos que deduzir ela, o que é exatamente o que a questão pede.
Para isto, teremos que relembrar a forma integral da definição de alongamento, dada por:
Para a nossa alegria, a força axial é uma constante e igual a . Nosso trabalho aqui será obter uma equação para a seção transversal variante.
OBS: a direção é a direção do comprimento da barra!!!
Passo 2
Vamos agora determinar a relação para a área da barra.
Como a barra tem seção retangular de espessura constante, a sua área será:
Sendo o uma função que varia linearmente de até . Portanto, como tem um comportamento linear, podemos escrevê-lo através de:
E assim chegamos a seguinte relação para a área:
Passo 3
Agora que determinamos a relação da área, basta substituirmos ela na nossa integral do Passo 1 e calcularmos ela.
Sendo assim, vamos aos cálculos:
E assim finalizamos a questão!