Um cabo vertical (ver a figura) sofre, na montagem, uma tração inicial de 450 kgf. Subsequentemente, coloca-se um peso de 700 kgf nesse cabo, em um ponto situado a uma altura em relação à base. Investigar as forças no cabo quando varia de 0 a L, sabendo que o cabo não pode suportar carga de compressão.
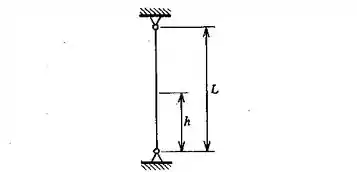
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos descobrir quais as forças internas no cabo quando se varia a posição de fixação do peso de 700 kgf.
Esta é uma questão semelhante a outras que já trabalhamos. O fato de termos uma corda não vai dificultar a nossa análise. Basta pensarmos que temos uma barra ao invés da corda e prosseguirmos da mesma forma que sempre fizemos.
Como temos um problema estaticamente indeterminado, vamos retirar um apoio e substituir por uma força. Fazendo isto, teremos o seguinte diagrama de equilíbrio:
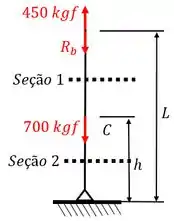
Temos uma força de tracionando a ponta do cabo, uma força de para baixo a uma altura , devido ao peso fixado no cabo, e uma reação , que surge após retirarmos o vínculo.
Para podermos determinar as forças no cabo, temos que descobrir primeiro quem é . Para isto, vamos ter que usar a restrição imposta no cabo devido aos dois vínculos: deformação total nula!
Passo 2
Agora é a hora de calcularmos a deformação total no cabo. Para isto, vamos calcular separadamente as deformações em cada seção, conforme indicado na figura do Passo 1.
Vamos começar pela seção 1. Desenhando o diagrama de equilíbrio, temos:
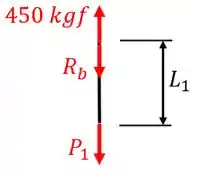
Portanto, como a barra está em equilíbrio , então, a força , força interna no cabo, é igual a . Assim, a deformação nesta seção será:
Agora, basta repetirmos para a outra seção! Esboçando o diagrama de equilíbrio para a seção 2, temos:
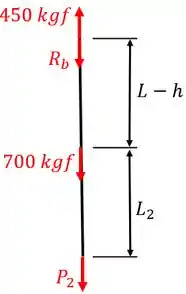
Para a seção 2, aplicando a relação de equilíbrio, obtemos . Portanto, a deformação devido a esta seção será:
Passo 3
Agora que já obtivemos as deformações das duas seções, já temos informação suficiente para descobrirmos quem é a força . Para isto, basta lembrarmos que a deformação total da barra deve ser igual a zero! Logo,
E assim conseguimos descobrir quem é a força como função de !
Passo 4
Para finalizarmos a questão, temos que descobrir quais são as forças internas no cabo.
Durante o Passo 2, nós descobrimos que a força interna na seção 1 era e na seção era . Ao substituirmos o valor de teremos:
Como (compressão) para todo , então, o cabo não suportará a carga de 700 kgf.
Resposta
O cabo não suportará a carga de 700 kgf.