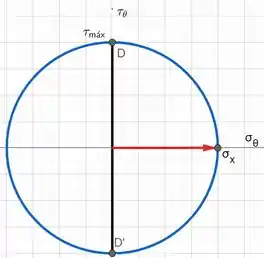
Desenhar o círculo de Mohr para o caso de cisalhamento puro (ver a Fig. 2.6) e, a partir da geometria do círculo, verificar a Eq. (2-17).

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

Precisamos desenhar o círculo de Mohr para o caso de cisalhamento puro. Então, antes de escrevermos a equação do nosso círculo, vamos identificar quais as tensões no nosso elemento.

Como temos cisalhamento puro, as tensões serão e .

Substituindo estes valores na equação do círculo de Mohr, temos:

Esboçando o círculo, temos:

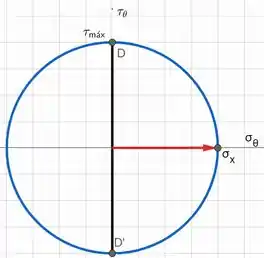
Como o círculo está centrado na origem, a distância do centro até é igual a distância até . Portanto, verificamos a relação 2.7, que nos diz que .

E assim finalizamos a questão!