Determina a força cortante e o momento fletor no meio da viga simplesmente apoiada, mostrada na Fig. 4-1a, sendo , e . Achar também a força cortante máxima e o momento fletor máximo.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos determinar a força cortante e o momento fletor no meio da viga da Fig. 4-1a e depois determinar quais os maiores valores dessa força e do momento na viga.
Bom, vamos começar a questão esboçando o diagrama de corpo livre da nossa viga. Sendo assim, teremos:
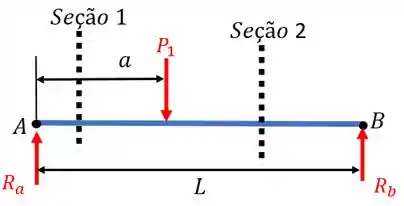
Para que a gente resolva a questão como todo, vamos ter que obter a relação de e para ambas as seções da nossa viga.
Então, agora que a gente já sabe o que fazer, vamos aos cálculos!
Passo 2
Nosso primeiro passo é obter as reações dos vínculos em e em . E para isto, basta utilizarmos as equações de equilíbrio da estática.
Portanto, fazendo o somatório de momentos em torno de e , temos:
Resolvendo o sistema acima chegamos a e
Passo 3
Agora vamos obter as relações para o momento fletor e esforço cortante de ambas as seções. Começando pela seção 1, fazendo um corte, temos:
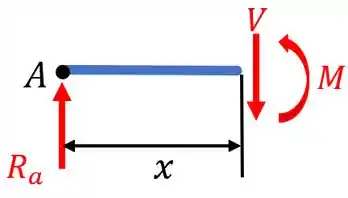
Sendo .
Agora, só precisamos aplicar as equações de equilíbrio. Portanto:
Já para a seção 2, ao realizarmos um corte, teremos o seguinte diagrama de corpo livre:
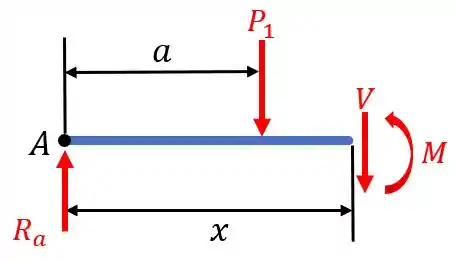
Sendo .
Agora, só precisamos aplicar as equações de equilíbrio. Portanto:
Passo 4
Agora a gente já tem informação suficiente para resolver tudo que a questão nos pediu.
No ponto médio da barra, quando , o esforço cortante e o momento fletor serão:
Já o esforço cortante e momento fletor máximo serão:
E assim finalizamos a questão!
Resposta
No ponto médio da barra, quando , o esforço cortante e o momento fletor serão:
Já o esforço cortante e momento fletor máximo serão: