Determinar a equação do eixo da barra curva, (ver a figura), antes da aplicação da carga, de modo que a carga aplicada, , movendo-se ao longo da barra, permaneça sempre no mesmo nível.
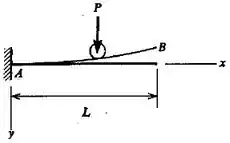
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta é uma questão que parece ser bem difícil. Mas depois que a gente saca a ideia, fica tranquila.
Precisamos mover a carga e manter o ponto de aplicação dela exatamente sobre o eixo . Portanto, a deflexão no ponto deve ser igual a posição da linha elástica.
Em outras palavras, imaginem que temos uma viga reta e nela aplicamos uma força a uma distância . A equação do eixo da barra é exatamente , sendo a deflexão da curva.
Para nossa alegria, no apêndice , temos a equação da linha elástica para uma força aplicada a uma distância . Ela é:
Se fizermos , teremos exatamente a deflexão para o caso da questão. Logo,
E como a equação da curva é , então, a resposta da questão será:
E assim finalizamos a questão!