(a) Determinar o módulo da seção necessária para uma viga simples, com de comprimento, capaz de suportar uma carga uniforme de e uma carga concentrada de no meio do vão. Considerar e desprezar o peso da viga. (b) Selecionar um perfil adequado, na tabela do apêndice, considerando o peso da viga.
Passo 1
Vamos começar!
O que nós sabemos?
Sabemos que as duas cargas, a uniforme e a concentrada, na viga vão gerar nela esforços internos na forma de forças cortantes e momentos fletores .
Esses momentos fletores vão gerar na viga tensões normais de flexão , de acordo com a fórmula da flexão:
Onde:
- (ou só “”) é o momento fletor em uma seção transversal da viga;
- é a posição do ponto da seção em que se quer calcular a tensão em relação à linha neutra da seção;
- & (ou só “”) é o momento de inércia da área da seção.
E o que é que o exercício quer?
Ele quer que a gente determine o módulo da seção necessária para a viga simples e selecione um perfil adequado às condições obtidas!
Passo 2
Então vamos começar encontrando os momentos fletores críticos na viga através dos métodos da estática!
Começando pelo primeiro passo dos métodos da estática, temos o DCL ou:
![]()
Para essa viga, feito o DCL... Temos que...

Passo 3
Por simetria, temos que...
Logo;
Passo 4
Encontrados os valores dos esforços externos atuantes na nossa viga, podemos seguir agora para a:
![]()
Então precisamos avaliar as duas seções da barra, que são a seção , entre e e a seção , entre e .
- Para a seção :
- Para a seção :
Assim...
Juntando tudo que acabamos de ver...
Conseguimos desenhar o diagrama de momento fletor abaixo para essa viga:
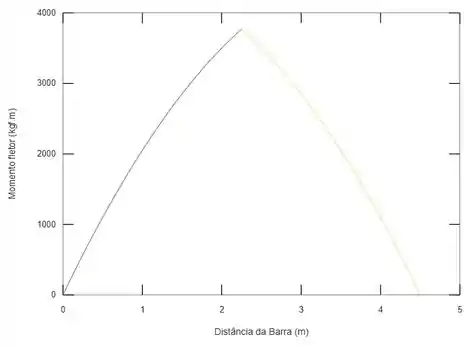
E tcharam! 😎
Desse diagrama de momento fletor, conseguimos retirar o valor crítico, que vai ser em ...
E assim terminamos toda a parte dos métodos da estática.
Passo 5
Com esses valores, vamos recorrer à fórmula abaixo...
Sabendo que...
Uma vez que conhecemos o ...
Convertendo para polegada cúbica, que é a unidade da nossa tabela...
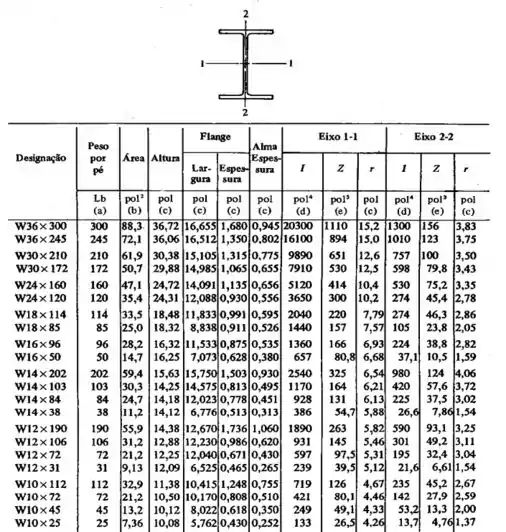
Podemos ver que a barra que chega mais perto é a ...
Diferiu um pouco!
Mas pode acreditar! Das que tem aí! É a que mais chega perto!
Resposta
a)
b)