O elemento, em estado duplo de tensão, mostrado na Fig. 2.5, tem deformações principais, e , nas direções e , respectivamente. Deduzir uma expressão para a deformação na direção de , exprimindo em termos de , e do ângulo . Comparar o resultado com a Eq. (2-7a) ou (2-8a).

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

Precisamos determinar a expressão para o cálculo de e depois comparar com a relação para a tensão .

A ideia para resolvermos esta questão é bem semelhante ao cálculo de . Enquanto para a tensão nós analisamos as tensões no plano inclinado para que o elemento mantivesse o equilíbrio, aqui temos que analisar o que acontece com o elemento antes e após a deformação de e .

Então, vamos começar desenhando um esboço do elemento antes e após a deformação. Vejamos só ele abaixo:

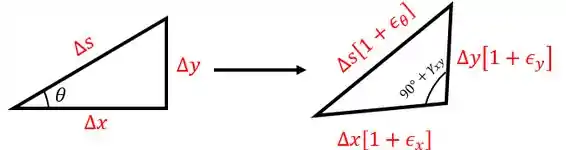
OBS: a deformação é uma deformação angular. Como a questão não falou nada deste parâmetro, vamos considerar que ele é nulo.

Então, o nosso triângulo após a deformação continuará sendo retângulo. Aplicando Pitágoras, temos:

Só que, da geometria antes da deformação, nós temos que e . Então,

Como e são valores muito pequenos, então, podemos desconsiderar os termos de segunda ordem e . Então,

E assim obtemos a nossa relação para . E ela é exatamente a relação para o cálculo de , a diferir apenas das tensões pelas deformações!

E assim finalizamos a questão!