Um elemento de material em estado de tensão simples é sujeito a uma tensão . Usando o círculo de Mohr, determinar as tensões num elemento para o qual .

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

Precisamos descobrir quais as tensões em um elemento rotacionado em , sendo que ele está sujeito apenas a uma tensão .

Então, vamos começar pelo círculo de Mohr. A sua equação será:

Esboçando o círculo com o estado inicial juntamente do estado do elemento após rotação temos:

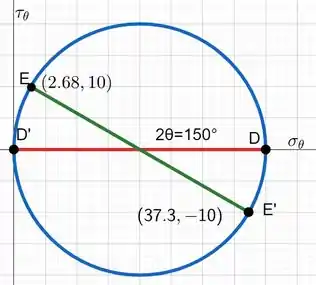
Como queremos uma rotação de 75° no sentido horário, no círculo temos que rotacionar também no sentido horário.

Ao encontrarmos a interseção da reta rotacionada com o círculo teremos o nosso estado de tensões. Neste caso, ele será:

E assim finalizamos a questão!