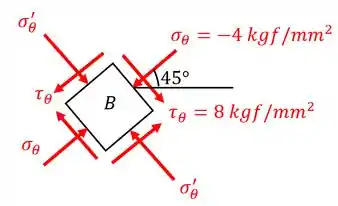
Para o exemplo dado na Fig. 2.8, determinar as tensões em um elemento que é girado de maneira que a tensão de cisalhamento seja máxima. (Mostrar os resultados desenhando o elemento.)

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

Para que a gente comece a resolver a questão, precisamos lembrar quais as tensões temos no exemplo da Fig. 2.8. Ao voltarmos lá podemos verificar que e .

Agora sim, com esses valores, já podemos partir para o círculo de Mohr.

Esboçando o círculo, temos:

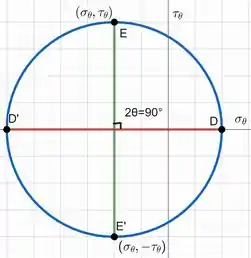
Agora que temos o círculo de Mohr conseguimos calcular as tensões para o estado de máxima tensão cisalhante. Ela será obtida após uma rotação de e terá as seguintes tensões: e . Esboçando o elemento, temos:

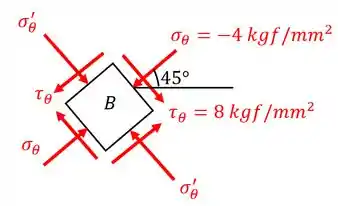
E assim finalizamos a questão!